ViBT: 노이즈 없는 생성의 시작, Vision Bridge Transformer (논문 리뷰)

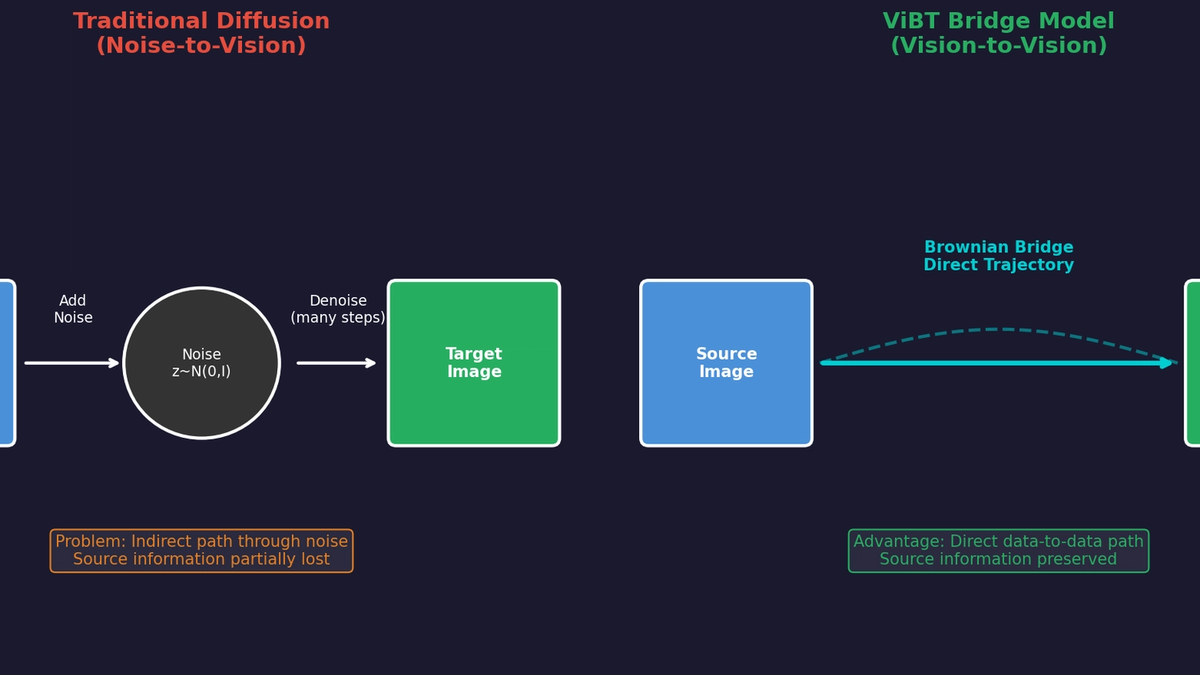
ViBT: 노이즈 없는 생성의 시작, Vision Bridge Transformer

들어가며

"이미지를 편집하려면 왜 노이즈로 갔다가 다시 돌아와야 할까?"

기존 Diffusion 모델들은 조건부 생성(Conditional Generation) 작업에서도 항상 Noise-to-Vision 패러다임을 따릅니다. 이미지 스타일 변환, 편집, Depth-to-Video 같은 작업에서도 먼저 노이즈를 만들고, 그 노이즈에서 결과물을 생성합니다.

하지만 곰곰이 생각해보면 이상합니다. 원본과 결과물이 비슷한 작업인데, 왜 굳이 정보를 다 날려버리는 노이즈 상태를 거쳐야 할까요?

ViBT(Vision Bridge Transformer)는 이 질문에서 출발합니다. Brownian Bridge라는 수학적 프레임워크를 사용하여, 소스에서 타겟으로 직접 연결되는 확률적 경로를 모델링합니다. 노이즈를 거치지 않고, 데이터에서 데이터로 직접 변환하는 Vision-to-Vision 패러다임입니다.

1. 핵심 문제 제기: 왜 노이즈를 거쳐야 하나?

1.1 기존 Diffusion의 비효율성

기존 Conditional Diffusion 모델의 작동 방식을 살펴봅시다:

문제점:

• 정보 손실: 소스 이미지의 정보를 노이즈로 완전히 파괴했다가 조건(condition)을 통해 다시 복원해야 합니다.
• 비직관적 경로: 스타일 변환처럼 원본과 유사한 결과물을 만들 때도, 완전히 다른 노이즈 상태를 거칩니다.
• 추론 비용: Condition Encoder가 별도로 필요하고, 이 토큰들이 계산량을 증가시킵니다.

1.2 Vision-to-Vision 패러다임의 필요성

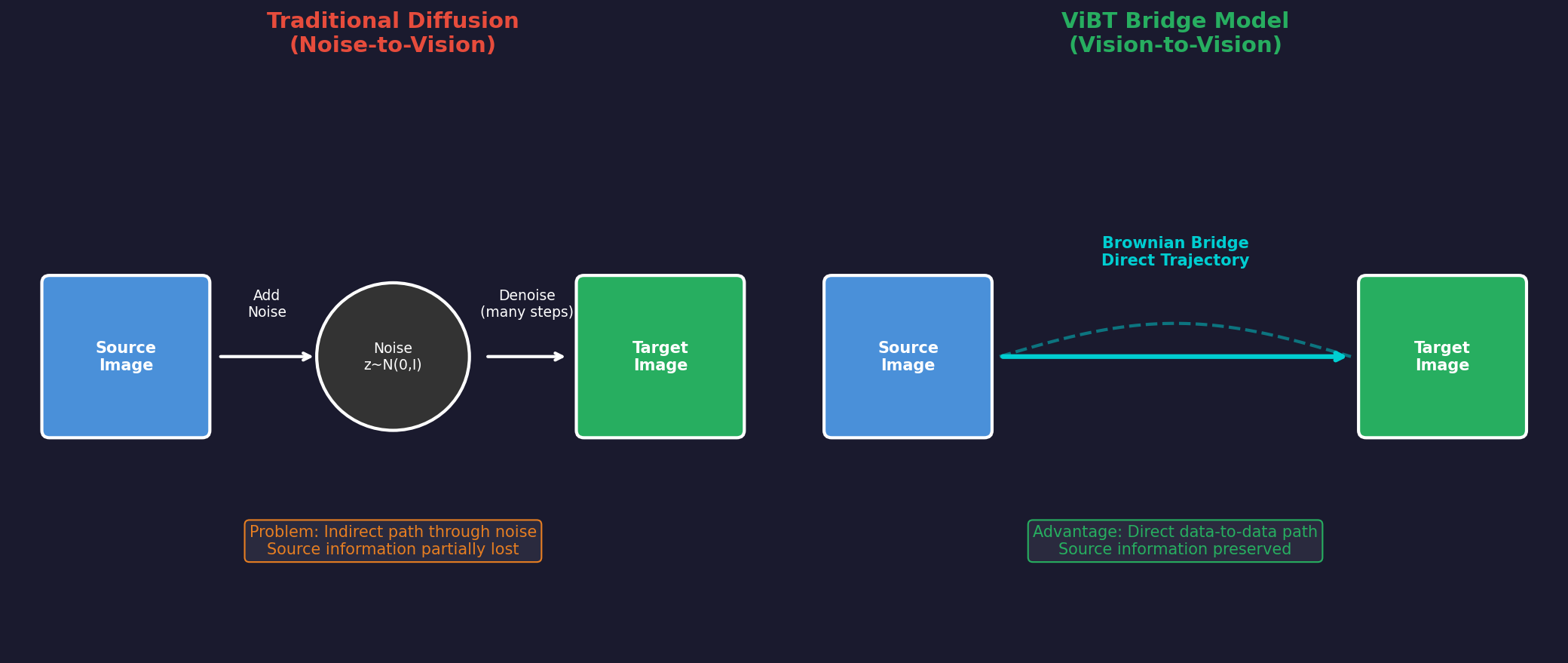
ViBT가 제안하는 새로운 관점:

"소스와 타겟이 비슷하다면, 그 사이를 직접 연결하는 경로를 학습하면 되지 않을까?"

이것이 바로 Bridge Model의 핵심 아이디어입니다.

2. Brownian Bridge: 수학적 기초

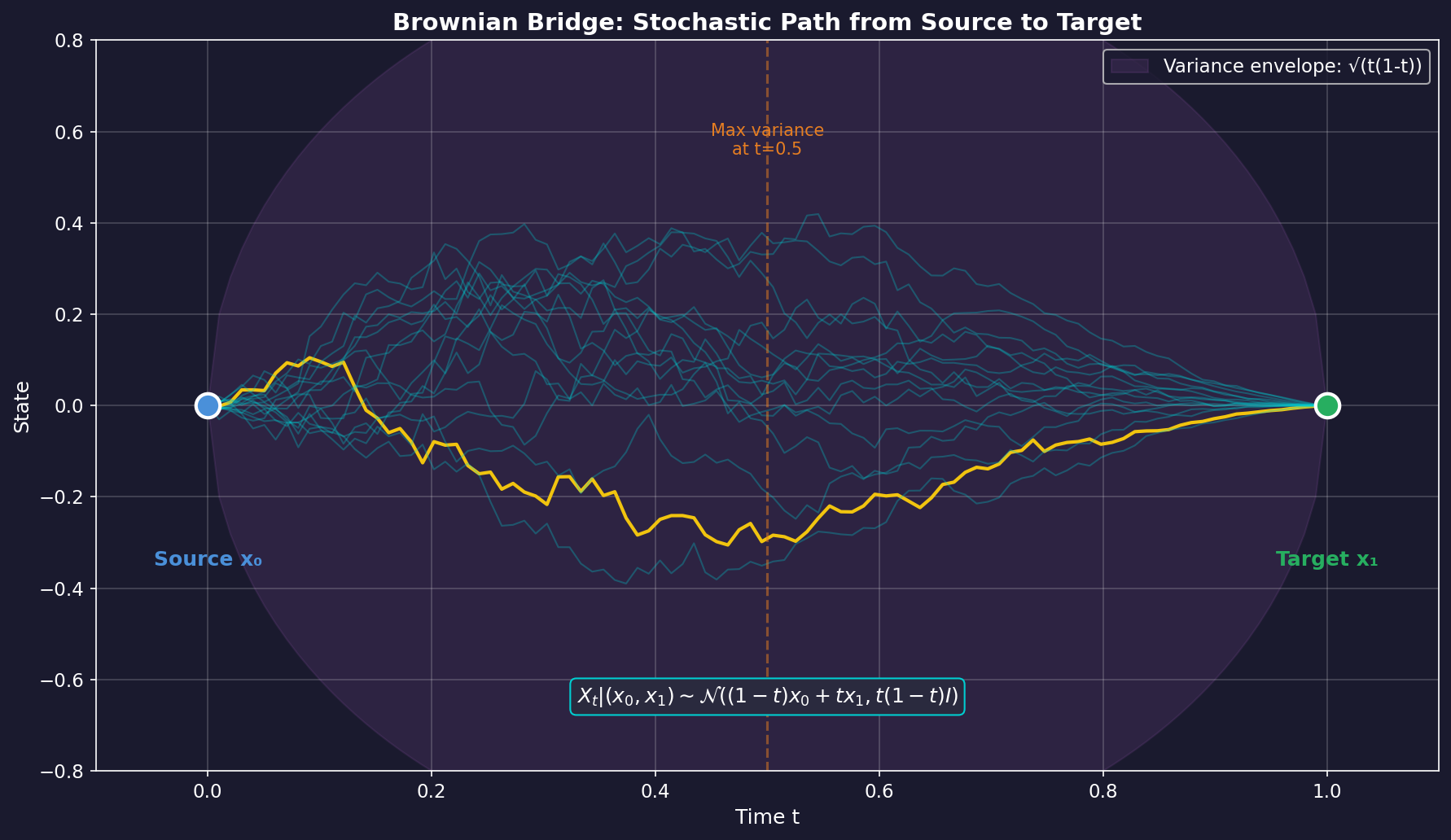
2.1 Brownian Bridge란?

Brownian Bridge는 양 끝점이 고정된 확률적 프로세스입니다. 일반적인 Brownian Motion이 시작점만 정해진 "자유로운 랜덤 워크"라면, Brownian Bridge는 시작점과 끝점이 모두 정해진 "구속된 랜덤 워크"입니다.

수학적 정의:

소스 $x_0$와 타겟 $x_1$이 주어졌을 때, 시간 $t$에서의 중간 상태 $X_t$는 다음 분포를 따릅니다:

$$X_t | (x_0, x_1) \sim \mathcal{N}((1-t)x_0 + tx_1, t(1-t)I)$$

핵심 특성:

• $t=0$: 정확히 $x_0$ (소스)
• $t=1$: 정확히 $x_1$ (타겟)
• $t=0.5$: 중간 상태, 분산이 최대

2.2 왜 Bridge가 효과적인가?

기존 Diffusion과의 결정적 차이:

Bridge 모델은 소스 정보를 경로의 일부로 직접 활용하기 때문에, 조건부 생성에서 더 효율적입니다.

3. ViBT의 기술적 혁신

3.1 문제: 대규모 학습의 불안정성

Bridge 모델을 20B 파라미터 규모로 확장하려면 심각한 문제가 발생합니다.

Velocity Target의 발산 문제:

Bridge의 순간 속도(velocity)는 다음과 같이 정의됩니다:

$$u_t(X_t|x_0, x_1) = \frac{x_1 - X_t}{1-t}$$

$t \rightarrow 1$일 때, 분모 $(1-t)$가 0에 가까워지면서 속도가 발산합니다. 이는 $O(1/\sqrt{1-t})$ 속도로 발산하며, 학습 손실이 불안정해지는 주요 원인입니다.

3.2 해결책: Stabilized Velocity Matching

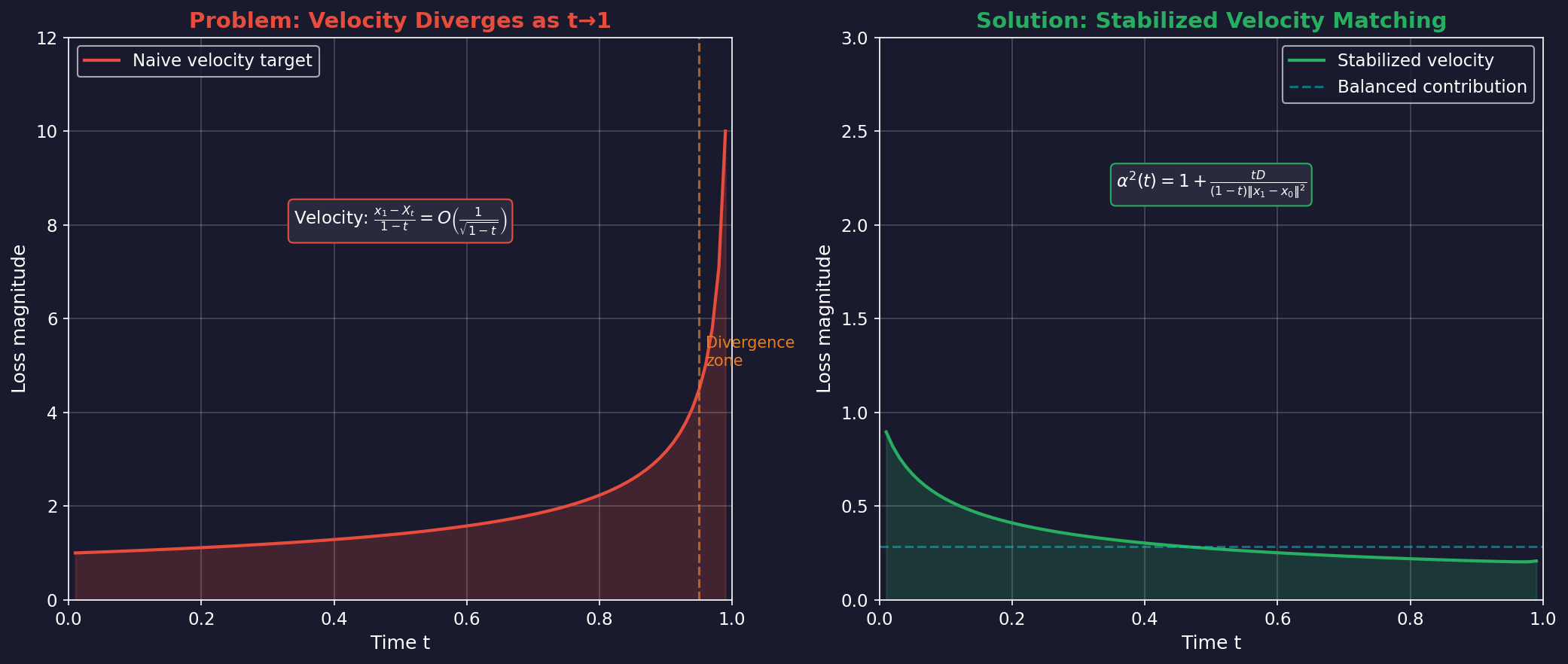
ViBT의 핵심 기여는 정규화 인자 α의 도입입니다:

$$\alpha(x_0, x_1, t)^2 = 1 + \frac{tD}{(1-t)\|x_1 - x_0\|^2}$$

여기서 $D$는 latent 차원입니다.

안정화된 학습 목표:

$$\mathcal{L}_{velocity} = \mathbb{E}\left[\left\|\frac{v_\theta(x_t, t) - u_t(x_t|x_1)}{\alpha}\right\|^2\right]$$

효과:

• $t$가 작을 때: $\alpha \approx 1$ (기존과 동일)
• $t \rightarrow 1$: $\alpha$가 커지면서 발산하는 velocity를 상쇄
• 결과: 모든 timestep에서 균형 잡힌 손실 기여

3.3 Variance-Corrected Sampling

학습뿐 아니라 추론 시에도 문제가 있습니다.

일반 Euler-Maruyama의 문제:

표준 이산화 방식은 Brownian Bridge의 분산 특성을 무시합니다. Bridge에서는 $t \rightarrow 1$로 갈수록 분산이 줄어들어야 하는데, 일반 샘플링은 이를 반영하지 못합니다.

ViBT의 수정된 샘플링:

$$x_{k+1} = x_k + \Delta t_k v_\theta(x_k, t_k) + \sqrt{\Delta t_k \cdot \frac{1-t_{k+1}}{1-t_k}} \epsilon_k$$

핵심은 노이즈 스케일에 $\frac{1-t_{k+1}}{1-t_k}$ 비율을 곱하는 것입니다. 이로써:

• 초기 ($t$ 작을 때): 높은 stochasticity
• 후기 ($t \rightarrow 1$): 낮은 stochasticity로 부드럽게 수렴

4. 아키텍처와 학습

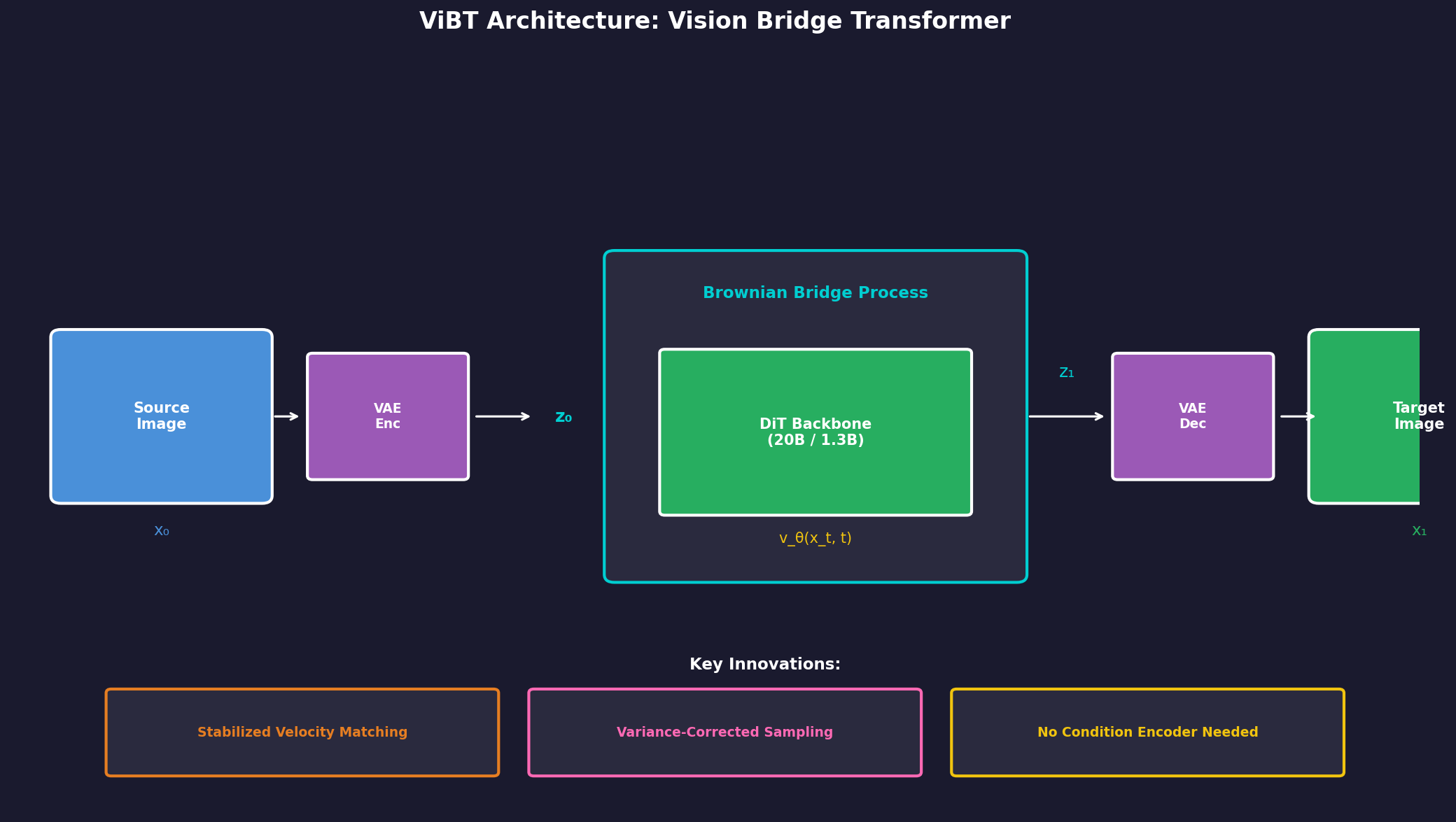
4.1 모델 구성

ViBT는 기존 DiT(Diffusion Transformer) 아키텍처를 기반으로 합니다:

이미지 모델 (20B):

• 베이스: Qwen-Image-Editing
• 미세조정: LoRA (rank 128)
• 학습: 20,000 iterations, 1 H100 GPU

비디오 모델 (1.3B):

• 베이스: Wan 2.1
• 미세조정: Full parameter
• 학습: 50,000 iterations, 4 H100 GPUs

4.2 학습 데이터

놀라운 점은 매우 적은 데이터로도 강력한 성능을 달성했다는 것입니다.

5. 실험 결과

5.1 벤치마크 성능

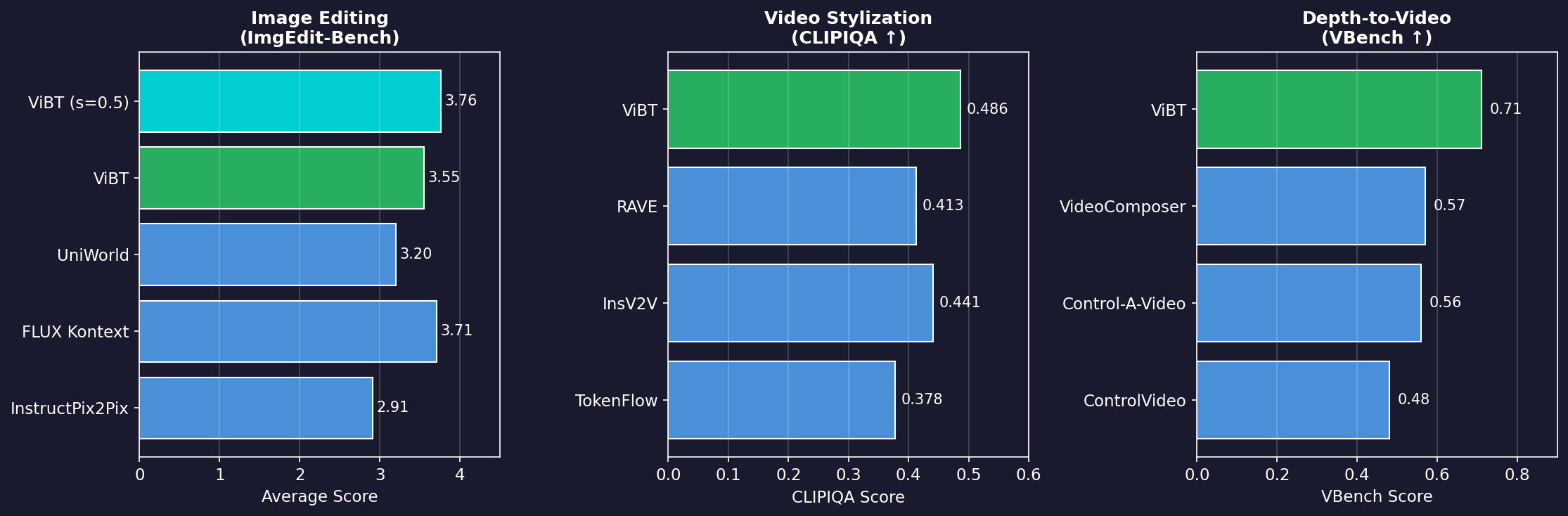
Image Editing (ImgEdit-Bench):

ViBT는 특히 Object Addition (4.20)과 Style Transfer (4.85)에서 뛰어난 성능을 보입니다.

Video Stylization:

Depth-to-Video:

5.2 속도 비교

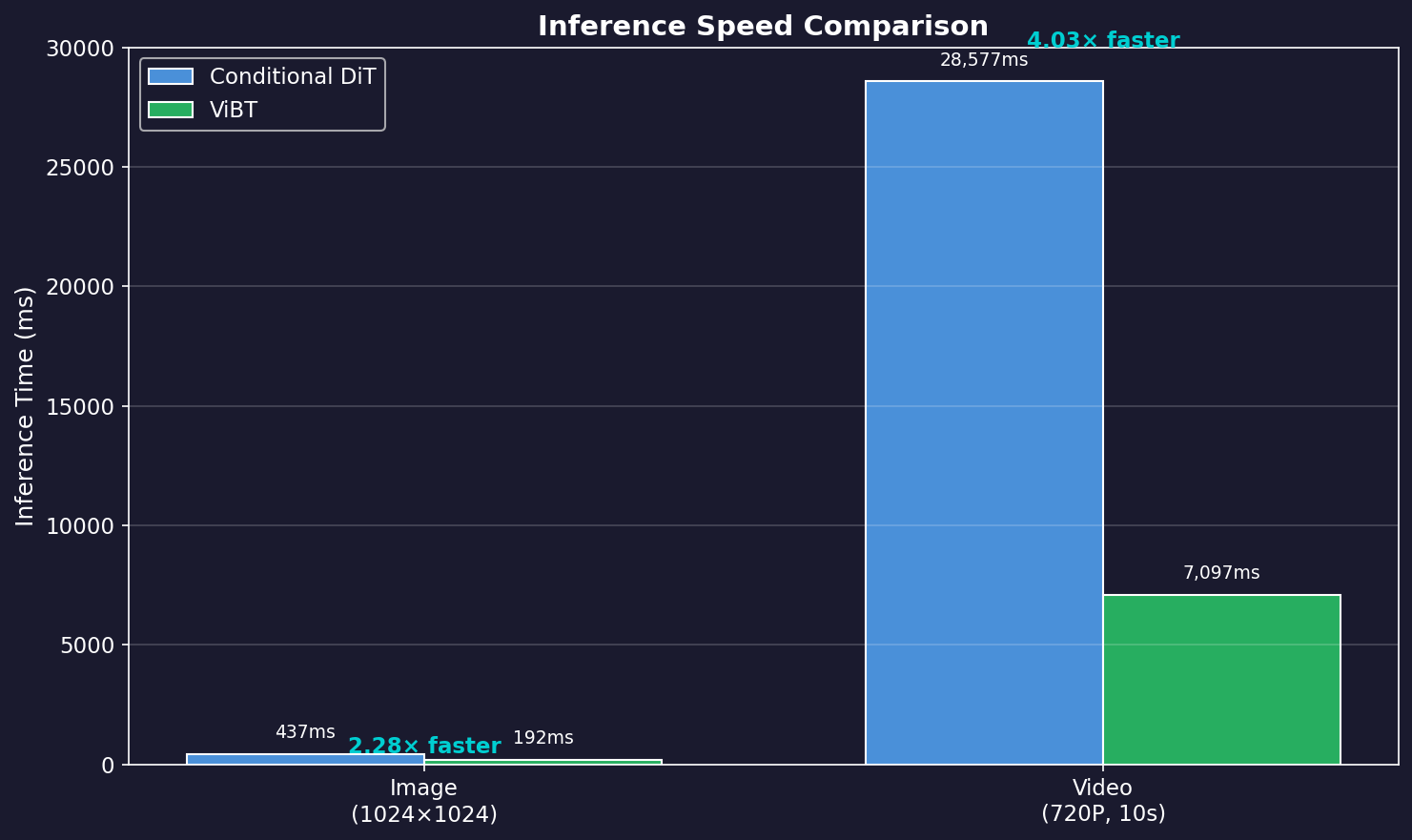
ViBT의 가장 큰 장점 중 하나는 추론 속도입니다:

속도 향상의 비밀:

• Condition Encoder 불필요
• 추가 conditioning 토큰 없음
• 약 50% 토큰 절감

6. Ablation Study: 노이즈 스케일의 영향

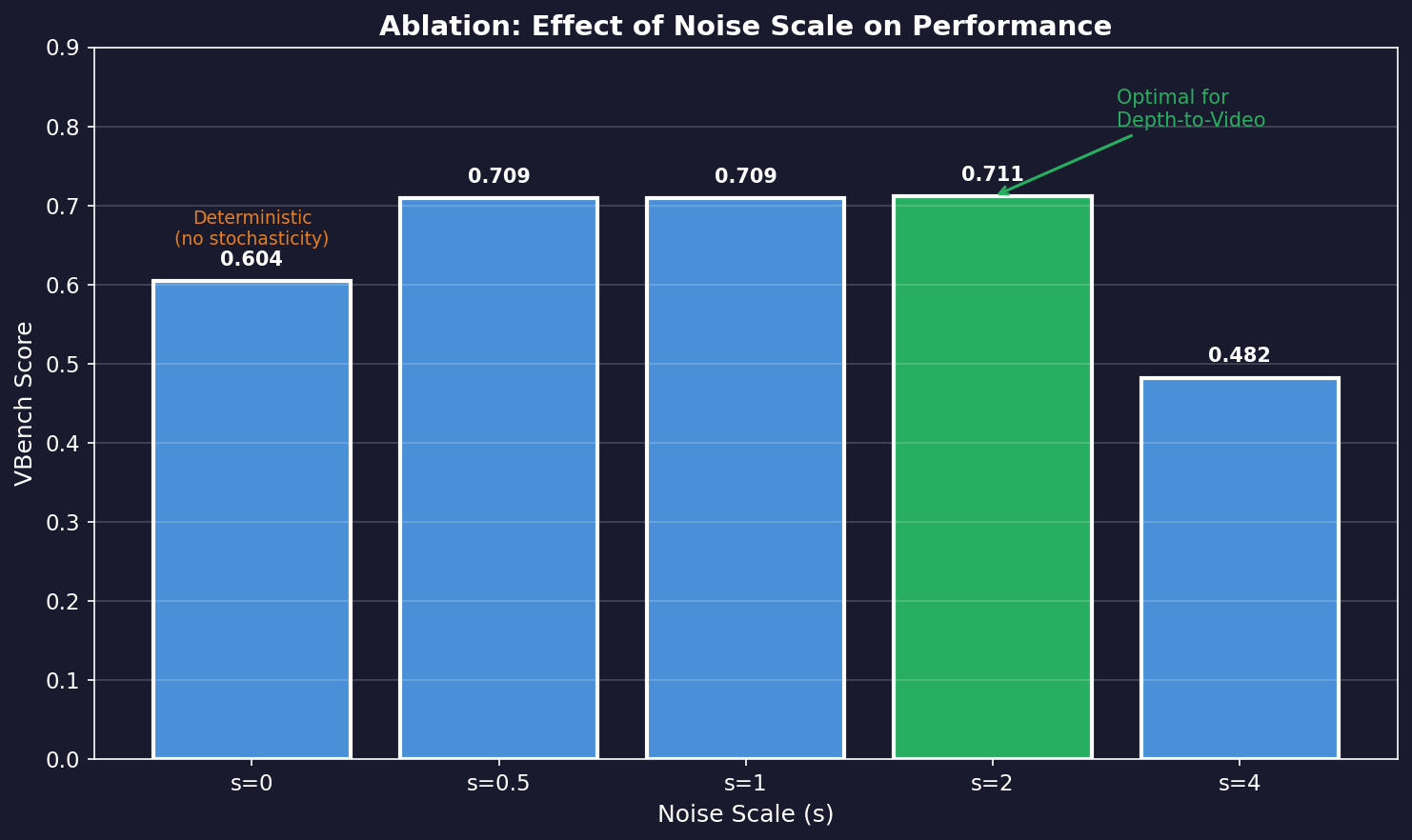
흥미로운 발견 중 하나는 최적의 노이즈 스케일이 태스크마다 다르다는 것입니다.

인사이트:

• $s=0$ (완전 결정론적): 성능 저하
• $s=2$ 근처: Depth-to-Video에 최적
• $s=0.5$: Image Editing에 최적
• $s=4$: 과도한 stochasticity로 성능 급락

이는 기존 연구들이 주장한 "극히 작은 노이즈 스케일이 최적"이라는 관점과 상반됩니다.

7. 한계점과 향후 방향

7.1 현재 한계

• 태스크별 노이즈 스케일 튜닝 필요: 아직 자동으로 최적 스케일을 찾는 방법은 없습니다.
• 복잡한 구조적 변화: 소스와 타겟이 매우 다른 경우 (예: 전혀 다른 구도로의 변환)에는 한계가 있을 수 있습니다.

7.2 향후 가능성

• 범용 Bridge 모델: 다양한 태스크를 단일 모델로 처리
• 더 큰 규모로의 확장: 100B+ 규모에서의 성능 검증
• 실시간 응용: 더 빠른 추론을 통한 인터랙티브 편집

8. 결론

ViBT는 조건부 생성 분야에서 패러다임 전환을 제안합니다:

1. Noise-free Generation: 노이즈를 거치지 않고 데이터에서 데이터로 직접 변환
2. Stabilized Training: 대규모 Bridge 모델 학습의 기술적 장벽 해결
3. Efficiency: Condition Encoder 없이 최대 4배 빠른 추론

특히 인상적인 것은 매우 적은 학습 데이터(수천 개 수준)로도 강력한 성능을 달성했다는 점입니다. 이는 Bridge 모델이 조건부 생성에서 본질적으로 효율적인 구조임을 시사합니다.

"노이즈 없이도 생성할 수 있다"는 ViBT의 메시지는, 향후 생성 모델 연구의 새로운 방향을 제시합니다.

참고 자료

• 논문 - arXiv:2511.23199: Tan et al., "Vision Bridge Transformer at Scale", 2025
• 프로젝트 페이지
• GitHub 저장소
• HuggingFace 데모