Latent Diffusion Models: The Core Principles of Stable Diffusion

TL;DR: Latent Diffusion performs diffusion in a compressed latent space instead of pixel space. This made high-resolution image generation practically possible and became the foundation technology for Stable Diffusion.

1. Why Latent Space?

1.1 The Problem with Pixel Space

Limitations of DDPM/DDIM:

Resolution	Pixels	U-Net Parameters	GPU Memory
64×64	12,288	~100M	~4GB
256×256	196,608	~400M	~16GB
512×512	786,432	~900M	~40GB
1024×1024	3,145,728	~2B	~160GB

Problem: Computation explodes at high resolution

1.2 Key Insight

Rombach et al.'s discovery:

"Most information in images lies in low-dimensional structures. High-frequency details are perceptually important but semantically redundant."

Intuition:

512×512 RGB image = 786,432 dimensions
But "meaningful" information fits in far fewer dimensions
Let's perform diffusion in this compressed representation!

1.3 Two-Stage Approach

Stage 1: Autoencoder (trained once) - The encoder compresses a 512×512×3 image into a 64×64×4 latent representation. The decoder reconstructs the image from this latent space back to 512×512×3.

Stage 2: Diffusion in Latent Space - The U-Net operates entirely in the compressed latent space, transforming noise into clean latents. The decoder then converts these clean latents into the final generated image.

2. Autoencoder: Image Compression

2.1 VAE (Variational Autoencoder)

LDM uses VAE to compress images:

Encoder $\mathcal{E}$ :

$z = \mathcal{E}(x) \in \mathbb{R}^{h \times w \times c}$

Decoder $\mathcal{D}$ :

$\hat{x} = \mathcal{D}(z) \approx x$

Compression Ratio (Stable Diffusion):

Input: 512×512×3 = 786,432
Latent: 64×64×4 = 16,384
48x compression!

2.2 VAE Training Objective

python

def vae_loss(x, z, x_recon, z_mean, z_logvar):
    # 1. Reconstruction Loss
    recon_loss = F.mse_loss(x_recon, x)

    # 2. Perceptual Loss (LPIPS)
    perceptual_loss = lpips(x_recon, x)

    # 3. KL Divergence (regularization)
    kl_loss = -0.5 * torch.mean(1 + z_logvar - z_mean.pow(2) - z_logvar.exp())

    # 4. Adversarial Loss (optional, for sharpness)
    adv_loss = discriminator_loss(x_recon)

    return recon_loss + 0.5 * perceptual_loss + 0.001 * kl_loss + 0.1 * adv_loss

2.3 KL-regularized Autoencoder

Differences from standard VAE:

Standard VAE:

$z \sim \mathcal{N}(\mu, \sigma^2)$ (sampling required)
Reconstruction can be blurry

LDM's KL-reg VAE:

Very small KL weight (0.00001)
Works nearly deterministically
Maintains sharp reconstruction

python

class KLRegularizedVAE(nn.Module):
    def __init__(self, ...):
        self.encoder = Encoder(...)
        self.decoder = Decoder(...)

    def encode(self, x):
        h = self.encoder(x)
        mean, logvar = h.chunk(2, dim=1)

        # Reparameterization (during training)
        std = torch.exp(0.5 * logvar)
        z = mean + std * torch.randn_like(std)

        return z, mean, logvar

    def decode(self, z):
        return self.decoder(z)

    def forward(self, x):
        z, mean, logvar = self.encode(x)
        x_recon = self.decode(z)
        return x_recon, mean, logvar

2.4 VQ-VAE Alternative

Some LDMs use VQ-VAE (Vector Quantized VAE):

$z_q = \text{Quantize}(z_e) = \arg\min_{e_k \in \mathcal{C}} || z_e - e_k ||$

Advantages:

Discrete latent space
Better reconstruction
No posterior collapse

Disadvantages:

Requires codebook training
Additional complexity

3. Latent Diffusion Process

3.1 Forward Process in Latent Space

Diffusion on latent $z = \mathcal{E}(x)$ instead of original image $x$ :

$q(z_t | z_0) = \mathcal{N}(z_t; \sqrt{\bar{\alpha}_t} z_0, (1 - \bar{\alpha}_t) I)$

3.2 Reverse Process

Denoising in latent space:

$p_\theta(z_{t-1} | z_t) = \mathcal{N}(z_{t-1}; \mu_\theta(z_t, t), \sigma_t^2 I)$

3.3 Training Objective

python

def ldm_training_step(model, vae, x, condition=None):
    # 1. Encode image to latent
    with torch.no_grad():
        z = vae.encode(x)

    # 2. Add noise
    t = torch.randint(0, T, (batch_size,))
    noise = torch.randn_like(z)
    z_t = sqrt(alpha_bar[t]) * z + sqrt(1 - alpha_bar[t]) * noise

    # 3. Predict noise
    noise_pred = model(z_t, t, condition)

    # 4. Loss
    loss = F.mse_loss(noise_pred, noise)

    return loss

3.4 Sampling

python

@torch.no_grad()
def ldm_sample(model, vae, shape, condition=None, num_steps=50):
    # 1. Start in latent space
    z = torch.randn(shape)  # (batch, 4, 64, 64)

    # 2. Diffusion reverse process (DDIM)
    for t in tqdm(reversed(range(num_steps))):
        noise_pred = model(z, t, condition)
        z = ddim_step(z, t, noise_pred)

    # 3. Decode latent to image
    images = vae.decode(z)

    return images

4. Conditioning Mechanisms

4.1 Cross-Attention for Text Conditioning

The key mechanism for injecting text conditions into U-Net:

$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d}}\right) V$

Where:

$Q$ : Generated from latent features
$K, V$ : Generated from text embeddings

python

class CrossAttention(nn.Module):
    def __init__(self, query_dim, context_dim, heads=8, dim_head=64):
        super().__init__()
        inner_dim = dim_head * heads

        self.to_q = nn.Linear(query_dim, inner_dim, bias=False)
        self.to_k = nn.Linear(context_dim, inner_dim, bias=False)
        self.to_v = nn.Linear(context_dim, inner_dim, bias=False)
        self.to_out = nn.Linear(inner_dim, query_dim)

        self.heads = heads
        self.scale = dim_head ** -0.5

    def forward(self, x, context):
        # x: (batch, seq_len, query_dim) - latent features
        # context: (batch, context_len, context_dim) - text embeddings

        q = self.to_q(x)
        k = self.to_k(context)
        v = self.to_v(context)

        # Multi-head reshape
        q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h=self.heads), (q, k, v))

        # Attention
        attn = torch.matmul(q, k.transpose(-1, -2)) * self.scale
        attn = F.softmax(attn, dim=-1)

        out = torch.matmul(attn, v)
        out = rearrange(out, 'b h n d -> b n (h d)')

        return self.to_out(out)

4.2 Text Encoder

Stable Diffusion uses CLIP text encoder:

python

class TextEncoder:
    def __init__(self, model_name="openai/clip-vit-large-patch14"):
        self.tokenizer = CLIPTokenizer.from_pretrained(model_name)
        self.model = CLIPTextModel.from_pretrained(model_name)

    def encode(self, text):
        tokens = self.tokenizer(
            text,
            padding="max_length",
            max_length=77,
            truncation=True,
            return_tensors="pt"
        )

        with torch.no_grad():
            embeddings = self.model(tokens.input_ids)[0]

        return embeddings  # (batch, 77, 768)

4.3 Classifier-Free Guidance (CFG)

The key technique for improving conditional generation quality:

$\tilde{\epsilon}_\theta = \epsilon_\theta(z_t, t, \emptyset) + w \cdot (\epsilon_\theta(z_t, t, c) - \epsilon_\theta(z_t, t, \emptyset))$

Where:

$w$ : guidance scale (typically 7.5)
$c$ : condition (text embedding)
$\emptyset$ : null condition (empty text)

python

def cfg_sample_step(model, z_t, t, text_emb, null_emb, guidance_scale=7.5):
    # Unconditional prediction
    noise_uncond = model(z_t, t, null_emb)

    # Conditional prediction
    noise_cond = model(z_t, t, text_emb)

    # CFG combination
    noise_pred = noise_uncond + guidance_scale * (noise_cond - noise_uncond)

    return noise_pred

5. U-Net Architecture for LDM

5.1 Overall Structure

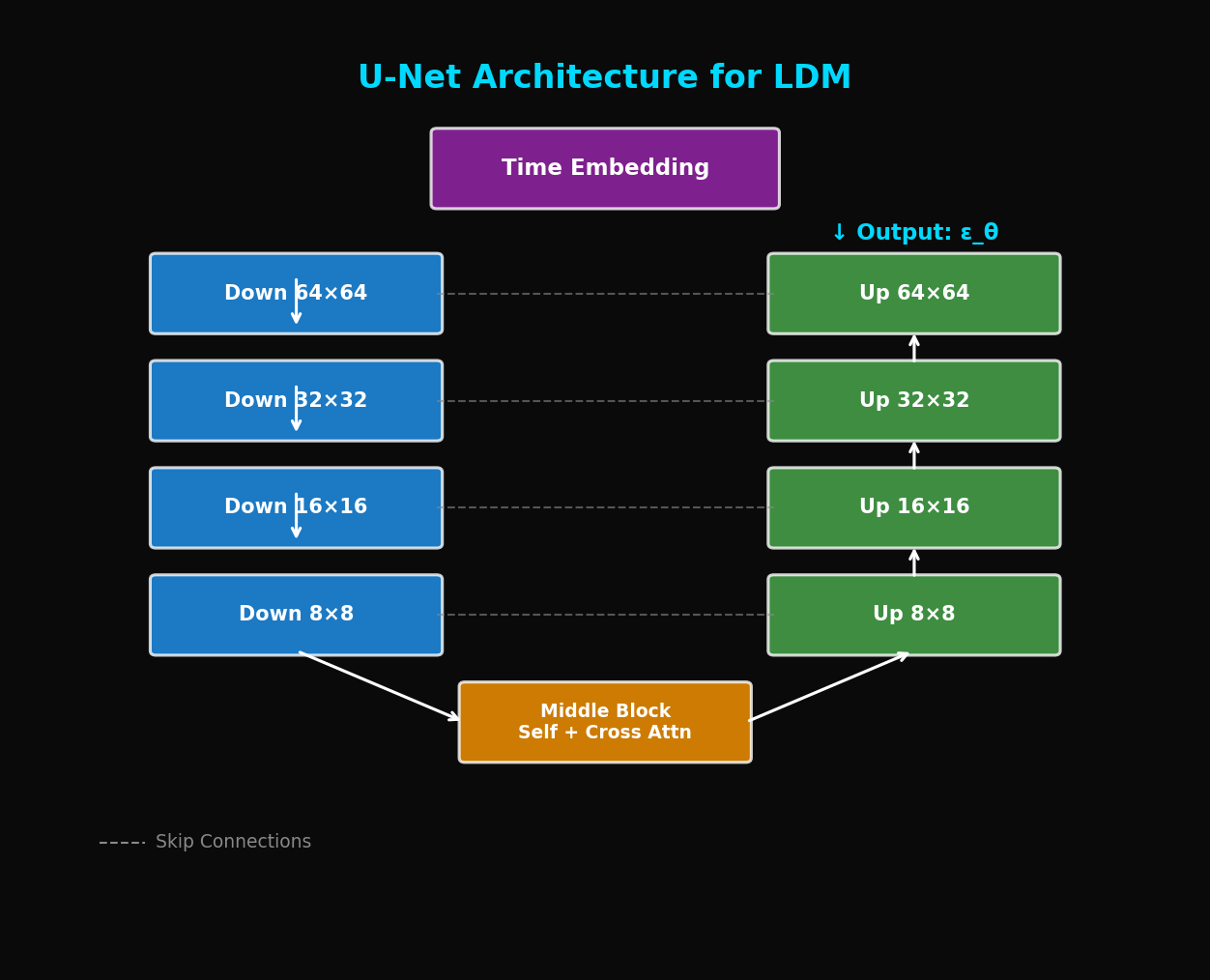
Input: z_t (64×64×4), t, text_emb

The U-Net architecture processes latents through three main stages: (1) Down Blocks with ResBlocks and Attention that progressively reduce spatial dimensions from 64×64 to 32×32 to 16×16 to 8×8, (2) a Middle Block containing ResBlock, Self-Attention, and Cross-Attention, and (3) Up Blocks with skip connections that restore spatial dimensions from 8×8 back to 64×64. Time embeddings condition every block, and the output predicts the noise ε_θ.

5.2 Transformer Block in U-Net

python

class BasicTransformerBlock(nn.Module):
    def __init__(self, dim, num_heads, context_dim):
        super().__init__()
        self.attn1 = CrossAttention(dim, dim, num_heads)  # Self-attention
        self.attn2 = CrossAttention(dim, context_dim, num_heads)  # Cross-attention
        self.ff = FeedForward(dim)

        self.norm1 = nn.LayerNorm(dim)
        self.norm2 = nn.LayerNorm(dim)
        self.norm3 = nn.LayerNorm(dim)

    def forward(self, x, context):
        # Self-attention (latent features attend to themselves)
        x = x + self.attn1(self.norm1(x), self.norm1(x))

        # Cross-attention (latent features attend to text)
        x = x + self.attn2(self.norm2(x), context)

        # Feed-forward
        x = x + self.ff(self.norm3(x))

        return x

5.3 ResBlock with Time Embedding

python

class ResBlock(nn.Module):
    def __init__(self, in_channels, out_channels, time_emb_dim):
        super().__init__()
        self.norm1 = nn.GroupNorm(32, in_channels)
        self.conv1 = nn.Conv2d(in_channels, out_channels, 3, padding=1)
        self.time_emb_proj = nn.Linear(time_emb_dim, out_channels)
        self.norm2 = nn.GroupNorm(32, out_channels)
        self.conv2 = nn.Conv2d(out_channels, out_channels, 3, padding=1)

        if in_channels != out_channels:
            self.skip_connection = nn.Conv2d(in_channels, out_channels, 1)
        else:
            self.skip_connection = nn.Identity()

    def forward(self, x, time_emb):
        h = self.norm1(x)
        h = F.silu(h)
        h = self.conv1(h)

        # Add time embedding
        h = h + self.time_emb_proj(F.silu(time_emb))[:, :, None, None]

        h = self.norm2(h)
        h = F.silu(h)
        h = self.conv2(h)

        return h + self.skip_connection(x)

6. Experimental Results

6.1 ImageNet 256×256

Model	FID ↓	IS ↑	Parameters
BigGAN	7.4	171.4	160M
ADM (pixel)	4.59	186.7	554M
LDM-4	3.60	247.7	400M

LDM achieves better performance with fewer parameters!

6.2 Text-to-Image (MS-COCO)

Model	FID ↓	CLIP Score ↑
DALL-E	27.5	-
GLIDE	12.2	0.32
Stable Diffusion	7.3	0.35

6.3 Computational Efficiency

Method	Resolution	Training (GPU days)	Sampling Time
ADM	256×256	2000	250s
LDM	256×256	100	10s
ADM	512×512	4000+	500s+
LDM	512×512	200	15s

20x more efficient training, 25x faster sampling

7. Stable Diffusion Architecture

7.1 Component Configuration

Stable Diffusion v1.5 specifications: VAE Encoder/Decoder (~84M parameters) with 8× compression (512→64) and 3→4 channels. U-Net (~860M parameters) with 64×64×4 input and attention at resolutions 32, 16, 8. Text Encoder uses CLIP ViT-L/14 (~123M parameters) with max 77 tokens. Total: approximately 1.1B parameters.

7.2 Complete Pipeline

python

class StableDiffusion:
    def __init__(self):
        self.vae = AutoencoderKL.from_pretrained("...")
        self.unet = UNet2DConditionModel.from_pretrained("...")
        self.text_encoder = CLIPTextModel.from_pretrained("...")
        self.scheduler = DDIMScheduler(...)

    @torch.no_grad()
    def generate(self, prompt, num_steps=50, guidance_scale=7.5):
        # 1. Text encoding
        text_emb = self.encode_text(prompt)
        null_emb = self.encode_text("")

        # 2. Initial latent
        latent = torch.randn(1, 4, 64, 64)

        # 3. Denoising loop
        self.scheduler.set_timesteps(num_steps)
        for t in self.scheduler.timesteps:
            # Classifier-free guidance
            latent_input = torch.cat([latent] * 2)
            text_input = torch.cat([null_emb, text_emb])

            noise_pred = self.unet(latent_input, t, text_input).sample
            noise_uncond, noise_cond = noise_pred.chunk(2)
            noise_pred = noise_uncond + guidance_scale * (noise_cond - noise_uncond)

            # Scheduler step
            latent = self.scheduler.step(noise_pred, t, latent).prev_sample

        # 4. Decode
        image = self.vae.decode(latent / 0.18215).sample

        return image

8. Advanced Techniques

8.1 ControlNet

Inject additional conditions (pose, edge, depth):

python

class ControlNet(nn.Module):
    def __init__(self, unet):
        super().__init__()
        # Clone U-Net's encoder part
        self.controlnet_encoder = copy.deepcopy(unet.encoder)

        # Zero convolution (zero output at initialization)
        self.zero_convs = nn.ModuleList([
            nn.Conv2d(ch, ch, 1) for ch in encoder_channels
        ])
        for conv in self.zero_convs:
            nn.init.zeros_(conv.weight)
            nn.init.zeros_(conv.bias)

    def forward(self, z_t, t, text_emb, control_image):
        # Pass control image through encoder
        control_features = self.controlnet_encoder(control_image, t)

        # Apply zero conv and add to U-Net
        control_outputs = [
            zero_conv(feat) for zero_conv, feat in zip(self.zero_convs, control_features)
        ]

        return control_outputs  # Added to U-Net's skip connections

8.2 LoRA (Low-Rank Adaptation)

Efficient fine-tuning:

python

class LoRALinear(nn.Module):
    def __init__(self, original_linear, rank=4, alpha=1.0):
        super().__init__()
        self.original = original_linear
        in_features = original_linear.in_features
        out_features = original_linear.out_features

        # Low-rank matrices
        self.lora_A = nn.Parameter(torch.randn(rank, in_features) * 0.01)
        self.lora_B = nn.Parameter(torch.zeros(out_features, rank))

        self.scale = alpha / rank

    def forward(self, x):
        original_out = self.original(x)
        lora_out = (x @ self.lora_A.T) @ self.lora_B.T * self.scale
        return original_out + lora_out

8.3 SDXL Improvements

Key changes in Stable Diffusion XL:

Component	SD 1.5	SDXL
Resolution	512×512	1024×1024
U-Net Parameters	860M	2.6B
Text Encoder	CLIP ViT-L	CLIP ViT-G + OpenCLIP ViT-bigG
Refiner	None	Separate model

9. Practical Tips

9.1 Prompt Engineering

python

# Good prompt example
good_prompt = """
a beautiful sunset over mountains,
highly detailed, 8k resolution,
professional photography,
golden hour lighting,
award winning photo
"""

# Bad prompt example
bad_prompt = "sunset mountains"

9.2 Using Negative Prompts

python

negative_prompt = """
blurry, low quality, distorted,
bad anatomy, watermark, signature,
out of frame, cropped
"""

# During generation
image = pipe(
    prompt=positive_prompt,
    negative_prompt=negative_prompt,
    guidance_scale=7.5
).images[0]

9.3 Optimal Parameters

Parameter	Recommended Range	Effect
guidance_scale	7-12	Higher = more prompt adherence
num_steps	20-50	More = higher quality, slower
seed	Fixed	Reproducibility

10. Conclusion

Latent Diffusion Models led the democratization of generative AI:

Efficiency: High resolution possible with 48x compression
Quality: Achieved SOTA FID/IS
Flexibility: Various conditioning possible
Accessibility: Runs on consumer GPUs

The open-source release of Stable Diffusion changed the landscape of image generation AI. In the next article, we'll cover DiT (Diffusion Transformer): a new paradigm replacing U-Net with Transformer.

References

Rombach, R., et al. (2022). High-Resolution Image Synthesis with Latent Diffusion Models. CVPR 2022
Podell, D., et al. (2023). SDXL: Improving Latent Diffusion Models for High-Resolution Image Synthesis. arXiv
Zhang, L., et al. (2023). Adding Conditional Control to Text-to-Image Diffusion Models. ICCV 2023
Hu, E., et al. (2022). LoRA: Low-Rank Adaptation of Large Language Models. ICLR 2022

Tags: #Latent-Diffusion #Stable-Diffusion #VAE #Cross-Attention #CFG #Text-to-Image #Deep-Learning

The complete code for this article is available in the attached Jupyter Notebook.